Towards a Mathematical Theory of Cortical Micro-circuits
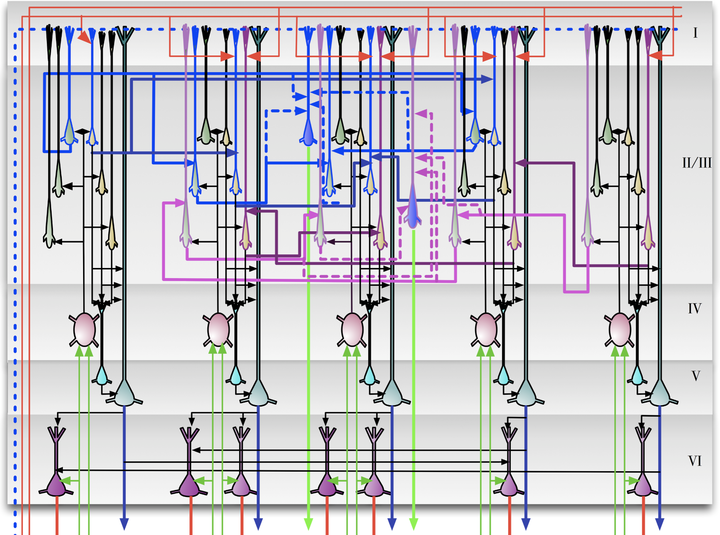 Image credit: Unsplash
Image credit: Unsplash
Abstract
The theoretical setting of hierarchical Bayesian inference is gaining acceptance as a framework for understanding cortical computation. In this paper, we describe how Bayesian belief propagation in a spatio-temporal hierarchical model, called Hierarchical Temporal Memory (HTM), can lead to a mathematical model for cortical circuits. An HTM node is abstracted using a coincidence detector and a mixture of Markov chains. Bayesian belief propagation equations for such an HTM node define a set of functional constraints for a neuronal implementation. Anatomical data provide a contrasting set of organizational constraints. The combination of these two constraints suggests a theoretically derived interpretation for many anatomical and physiological features and predicts several others. We describe the pattern recognition capabilities of HTM networks and demonstrate the application of the derived circuits for modeling the subjective contour effect. We also discuss how the theory and the circuit can be extended to explain cortical features that are not explained by the current model and describe testable predictions that can be derived from the model.